Skip to main content

A Guide to The New Statistics with R

17 Binomial GLMs

17.1 Binomial counts and proportion data

  • Binomial counts arise when the data are comprised of variables in which there is a known number of occasions (binomial trials) on which something of interest could occur
    • We know how many times something happened (successes) and how many times it did not (failures)
      • The sucesses + failures sum give the binomial denominator
  • Binomial count data can be expressed as proportions (that is, the proportion of successes)
  • But if the binomial denominator (the number of trials) varies then it is better to use binomial count data because all trials are weighted equally
  • When the size of the trials is not recorded, then proportion version of the data must be used
install.packages("arm",  repos = "https://cran.us.r-project.org")
install.packages("ggplot2",  repos = "https://cran.us.r-project.org")
install.packages("dplyr",  repos = "https://cran.us.r-project.org")
install.packages("AICcmodavg",  repos = "https://cran.us.r-project.org")

17.2 The beetle data

  • For this chapter, we will focus on data from an experiment that examined mortality rates of eight batches of the flour beetle Tribolium confusa when these groups were exposed to different doses of a pesticide (carbon disulfide) in 1935
  • Insecticide treatment lasted 5 hours
  • The unit for Dose is \(mg \cdot L^{-1}\) 
data("beetle")
beetle
#>    Dose Number_tested Number_killed Mortality_rate
#> 1 49.06            49             6      0.1224490
#> 2 52.99            60            13      0.2166667
#> 3 56.91            62            18      0.2903226
#> 4 60.84            56            28      0.5000000
#> 5 64.76            63            52      0.8253968
#> 6 68.69            59            53      0.8983051
#> 7 72.61            62            61      0.9838710
#> 8 76.54            60            60      1.0000000

Change column names:

names(beetle)[2] <- "tested"
names(beetle)[3] <- "killed"
names(beetle)
#> [1] "Dose"           "tested"         "killed"        
#> [4] "Mortality_rate"

Add a column for number of individuals that survived the pesticide treatment:

beetle$alive <- beetle$tested - beetle$killed
head(beetle)
#>    Dose tested killed Mortality_rate alive
#> 1 49.06     49      6      0.1224490    43
#> 2 52.99     60     13      0.2166667    47
#> 3 56.91     62     18      0.2903226    44
#> 4 60.84     56     28      0.5000000    28
#> 5 64.76     63     52      0.8253968    11
#> 6 68.69     59     53      0.8983051     6
  • A binomial GLM will investigate the number of beetles killed (successes) out of the number tested (the binomial denominator) as a function of dose of insecticide (concentration in \(mg \cdot L^{-1}\))
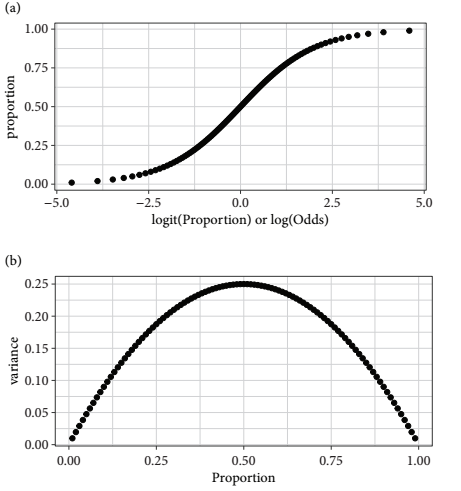
  • When binomial count data are expressed in proportions, they are bounded by (0,1)
    • The floor and ceiling of values constrain the variance
  • The expected means require some form of S-shaped relationship for a model of the mean
    • The variance decreases towards the extremes (0 and 1) and is greatest in between
  • A GLM using the binomial distribution with the logistic curve (the default link function) models the mean with a symmetric S-shape

17.2.1 Logits and the logistic curve

  • The logistic transformation converts proportions to logits
    • Logits are natural logs of the odds, which are the ratio of successes to failures
    • For a binomial denominator of 10 with five successes and five failures, the logit is \(log(5/5) = 0\)
  • One logit worth remembering is that a proportion of 0.5 is a logit of zero
    • Negative logits correspond to proportions less than 0.5
    • Positve logits correspond to proportions greater than 0.5
  • Logistic transformations map proportions from zero to one onto a symmetric S-shaped curve that asymptotes towards \(\pm\infty\)

17.3 GLM for binomial counts

  • The GLM of the binomial counts analyses the number beetles killed in each batch while taking into account the size of each group
  • The numbers of successes and failures must be bound together so that they can be jointly supplied as the response variable in the binomial GLM model formula

Create model for binomial count data:

m1_logit <- glm(cbind(killed, alive) #written as (successes, failures) as we are interested in mortality rate
                ~ Dose, data = beetle,
                family = binomial(link = "logit"))

Extract the regression intercept and slope of the line (linear on the logit scale):

coef(m1_logit)
#> (Intercept)        Dose 
#> -14.5780604   0.2455399

Zero falls way outside of the 95% CI, we can probably reject the null hypothesis that there is not a dose dependent relationship with beetle mortality rate:

confint(m1_logit)
#> Waiting for profiling to be done...
#>                   2.5 %      97.5 %
#> (Intercept) -17.2645230 -12.1608424
#> Dose          0.2056099   0.2900912

The display() function provides the same result in different form:

display(m1_logit)
#> glm(formula = cbind(killed, alive) ~ Dose, family = binomial(link = "logit"), 
#>     data = beetle)
#>             coef.est coef.se
#> (Intercept) -14.58     1.30 
#> Dose          0.25     0.02 
#> ---
#>   n = 8, k = 2
#>   residual deviance = 8.4, null deviance = 267.7 (difference = 259.2)

Model formula for an equivalent analysis - a weighted GLM on proportion data:

m2 <- glm(Mortality_rate ~ Dose, data = beetle,family = binomial, #mortality rate as a function of dosage
          weight = tested) #ensures that group size is taken into account 
summary(m2)
#> 
#> Call:
#> glm(formula = Mortality_rate ~ Dose, family = binomial, data = beetle, 
#>     weights = tested)
#> 
#> Deviance Residuals: 
#>     Min       1Q   Median       3Q      Max  
#> -1.3456  -0.4515   0.7929   1.0422   1.3262  
#> 
#> Coefficients:
#>              Estimate Std. Error z value Pr(>|z|)    
#> (Intercept) -14.57806    1.29846  -11.23   <2e-16 ***
#> Dose          0.24554    0.02149   11.42   <2e-16 ***
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 267.6624  on 7  degrees of freedom
#> Residual deviance:   8.4379  on 6  degrees of freedom
#> AIC: 38.613
#> 
#> Number of Fisher Scoring iterations: 4
  • The coefficents of models m1 and m2 are the same
  • We can use the weighted GLM to help plot the data:

It is more clear to plot mortality rate as a proportion:

fig17_2 <- ggplot(beetle, aes(x = Dose, y = Mortality_rate)) + 
  xlab("Dose (mg/L)") + ylab("Mortality rate") + 
  geom_point() + 
   geom_smooth(method = "glm", method.args = list(binomial), aes(weight = tested)) + 
  scale_x_continuous(limits = c(45, 80),
                     breaks = seq(45, 80, by = 5))
fig17_2
#> `geom_smooth()` using formula 'y ~ x'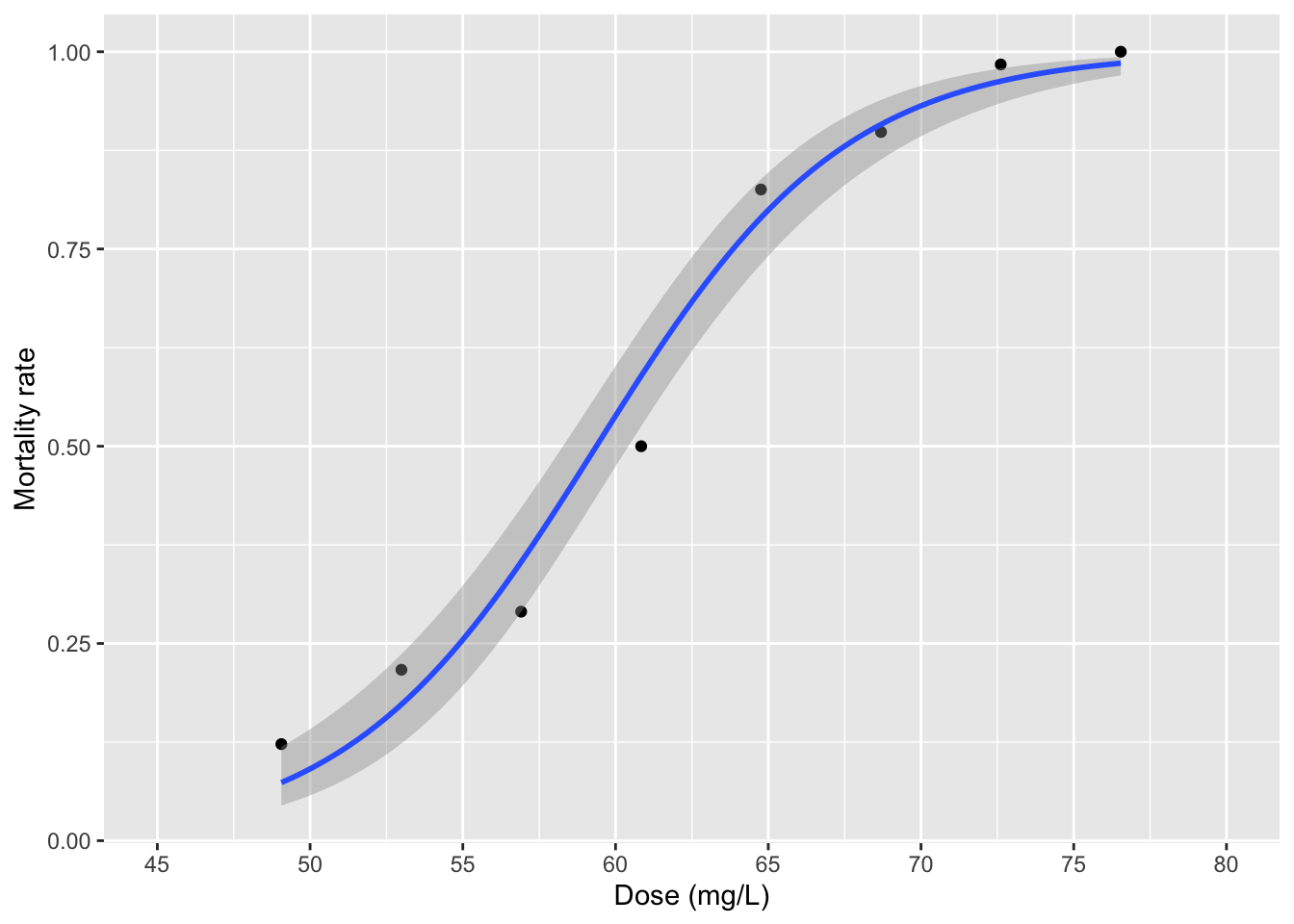
  • Referring back to the summary() output table, we see that the ratio of residual deviance to degrees of freedom is 8.4379:6 giving us a dispersion parameter of approximately 1.4
    • The author says that the data are not too overdispersed, but since the index value is above the rule of thumb value of 1.2 for overdispersed data, we can account for it using a quasi-maximum likelihood approach

Quasi-binomial approach baked into model:

m1_quasi <- glm(cbind(killed, alive) 
                ~ Dose, data = beetle,
                family = quasibinomial)
summary(m1_quasi)
#> 
#> Call:
#> glm(formula = cbind(killed, alive) ~ Dose, family = quasibinomial, 
#>     data = beetle)
#> 
#> Deviance Residuals: 
#>     Min       1Q   Median       3Q      Max  
#> -1.3456  -0.4515   0.7929   1.0422   1.3262  
#> 
#> Coefficients:
#>              Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) -14.57806    1.46611  -9.943 5.98e-05 ***
#> Dose          0.24554    0.02427  10.118 5.42e-05 ***
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for quasibinomial family taken to be 1.274895)
#> 
#>     Null deviance: 267.6624  on 7  degrees of freedom
#> Residual deviance:   8.4379  on 6  degrees of freedom
#> AIC: NA
#> 
#> Number of Fisher Scoring iterations: 4
  • This summary output table gives a specific like for the dispersion parameter and it is lower than it was previously
  • The standard errors are a little bit larger
  • No AIC value is provided