19 Conclusions

19.1 Introduction

This text began with an analysis of the Space Shuttle Challenger distaster
The author concludes the book by re-analyzing the data using keypoints covered in the past 17 chapters

install.packages("arm",  repos = "https://cran.us.r-project.org")
install.packages("ggplot2",  repos = "https://cran.us.r-project.org")
install.packages("faraway",  repos = "https://cran.us.r-project.org")
install.packages("patchwork",  repos = "https://cran.us.r-project.org")
install.packages("dplyr",  repos = "https://cran.us.r-project.org")
install.packages("Sleuth3",  repos = "https://cran.us.r-project.org")

library(arm)
library(ggplot2)
library(faraway)
library(dplyr)
library(patchwork)
library(Sleuth3)

19.2 A binomial GLM analysis of the Challenger binary data

The fuel leaks key to this dataset can be expressed in binary form

urlfile="https://raw.githubusercontent.com/apicellap/data/main/ex2011.csv"
ex2011x<-read.csv(url(urlfile))
str(ex2011x)
#> 'data.frame':    24 obs. of  2 variables:
#>  $ Temperature: int  53 56 57 63 66 67 67 67 68 69 ...
#>  $ Failure    : chr  "Yes" "Yes" "Yes" "No" ...

head(ex2011x)
#>   Temperature Failure
#> 1          53     Yes
#> 2          56     Yes
#> 3          57     Yes
#> 4          63      No
#> 5          66      No
#> 6          67      No

This dataset contains an error, rectify it:

ex2011x[4,2] <- "Yes" #It is always better document changes in a script and not alter the original dataframe

Plot Failure vs. launch temperature:

fig19_1 <- ggplot(ex2011x, aes(x = Temperature, y = Failure)) + geom_point()
fig19_1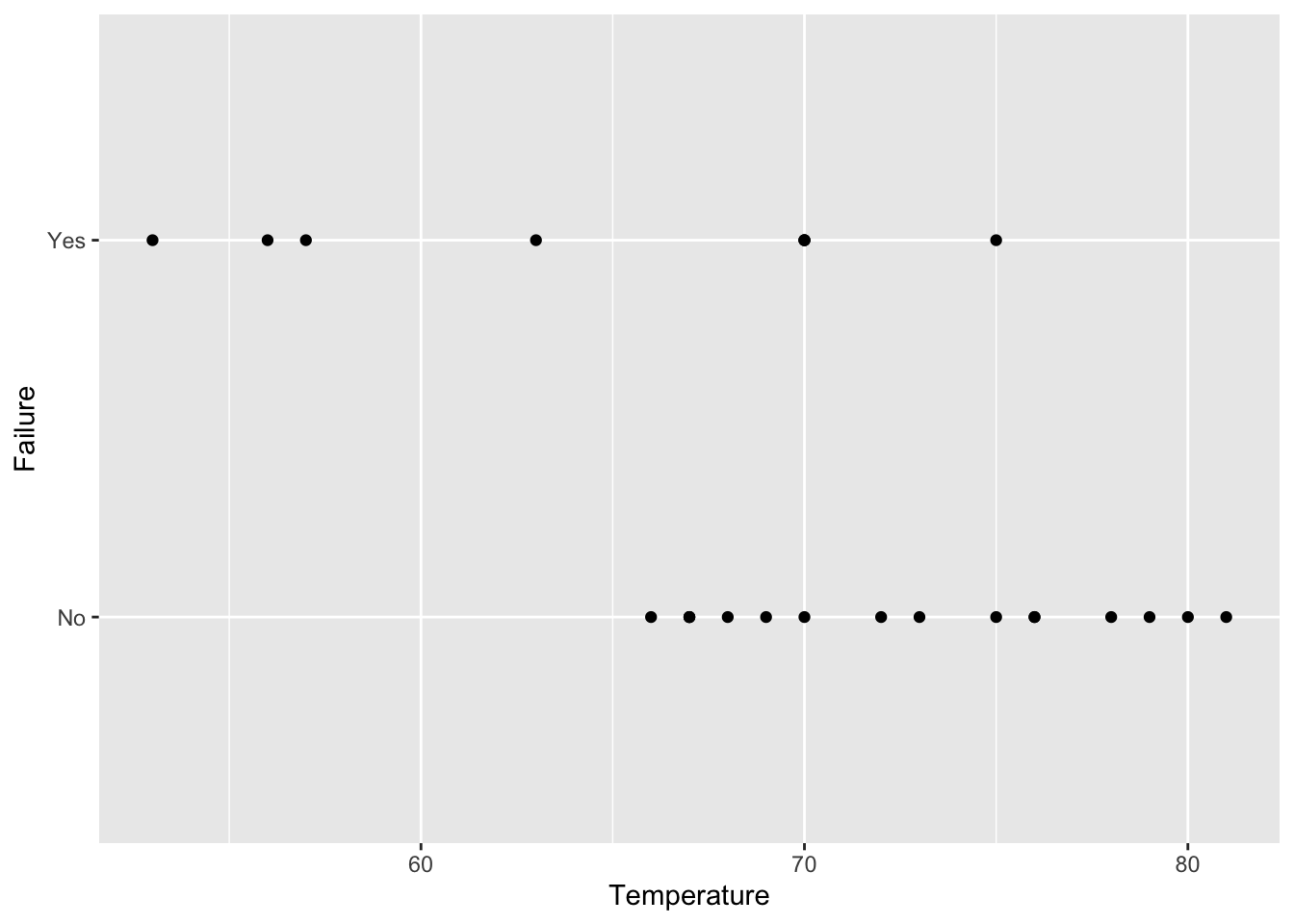

Recharacterize binary form of data:

ex2011x <- ex2011x %>% 
  mutate(failure = if_else(ex2011x$Failure == "Yes",1 , 0)) #if this statement is true then in column entitled 'failure' put 1, else put 0 
head(ex2011x)
#>   Temperature Failure failure
#> 1          53     Yes       1
#> 2          56     Yes       1
#> 3          57     Yes       1
#> 4          63     Yes       1
#> 5          66      No       0
#> 6          67      No       0

Create a binomial GLM:

m1 <- glm(failure ~ Temperature, family = binomial(link = "logit"), data = ex2011x)

Extract the model’s coefficients:

coef(m1)
#> (Intercept) Temperature 
#>  14.1700665  -0.2155279

Examine the 95% CI:

confint(m1)
#> Waiting for profiling to be done...
#>                  2.5 %      97.5 %
#> (Intercept)  3.3162485 31.83327461
#> Temperature -0.4724172 -0.05831438

Based on the negative slope and the 95% CI, there is clearly a relationship between failure and temperature
- The probability of a fuel leak increases in colder conditions

Plot the relationship:

fig19_2 <- ggplot(ex2011x, aes(x = Temperature, y = failure)) + geom_point() + 
  geom_smooth(method = "glm", method.args = list(family = "binomial"))
fig19_2
#> `geom_smooth()` using formula 'y ~ x'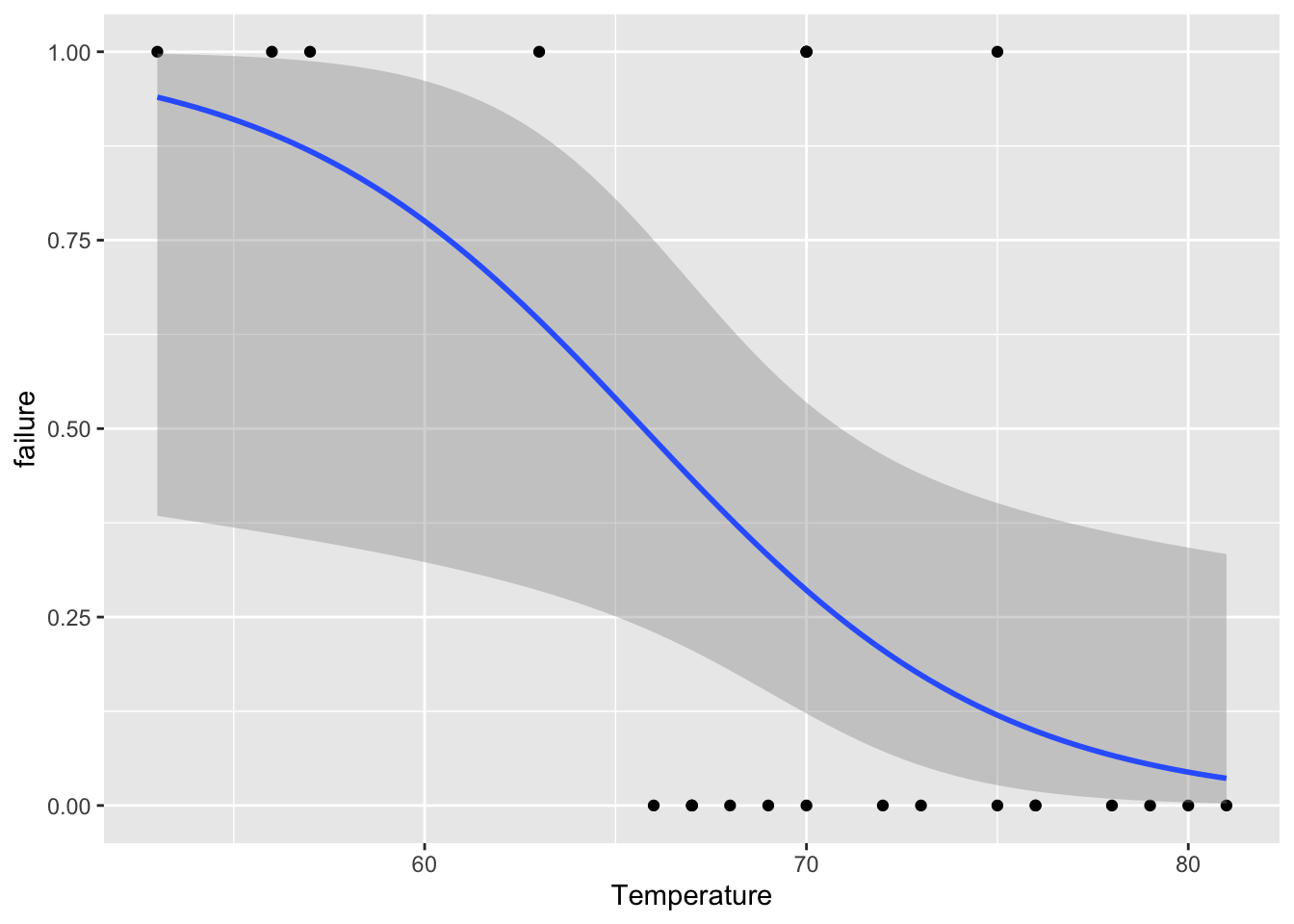

The plot shows a wide degree of uncertainty around the regression line
Even though there is a lot of uncertainty, the uncertainty encompasses a high degree for the system to fail
The temperature at the day of catastrophic launch was 30 degrees, which is well below the scope of the model
Still we can extrapolate from the data (taking with it a large grain of salt) through the binomial GLM

Taking sample size into account we can get the t value for a two-tailed 95% CI when n = 21:

t21 <- qt(0.975, 21)
t21
#> [1] 2.079614

Use the predict() function to make predictions from the GLM:

predicts <- predict(m1, data.frame(Temperature = 30:85), 
                    se = TRUE)

Create a dataframe of predicted ranges of values around the regression curve

fit <- ilogit(predicts$fit) #ilogit() back transforms from logit to probability values 
upper <- ilogit(predicts$fit + t21 * predicts$se.fit)
lower <-ilogit(predicts$fit - t21 * predicts$se.fit)
predictions <- data.frame(fit, upper, lower, Temperature = 30:85)
head(predictions)
#>         fit     upper     lower Temperature
#> 1 0.9995493 0.9999999 0.4150330          30
#> 2 0.9994409 0.9999998 0.4122349          31
#> 3 0.9993066 0.9999997 0.4094173          32
#> 4 0.9991399 0.9999995 0.4065783          33
#> 5 0.9989333 0.9999992 0.4037160          34
#> 6 0.9986771 0.9999988 0.4008283          35

Redraw the figure with extrapolated probability values for the new range of Temperature values:

fig19_3 <- ggplot(ex2011x, aes(x = Temperature, y = failure)) + 
  xlim(30, 80) + 
  geom_point() + 
  geom_line(data = predictions, aes(Temperature, fit), colour = "blue") + 
  geom_line(data = predictions, aes(Temperature, upper), colour = "darkgrey") + 
  geom_line(data = predictions, aes(Temperature, lower), colour = "darkgrey") 
fig19_3
#> Warning: Removed 1 rows containing missing values
#> (geom_point).
#> Warning: Removed 5 row(s) containing missing values (geom_path).
#> Removed 5 row(s) containing missing values (geom_path).
#> Removed 5 row(s) containing missing values (geom_path).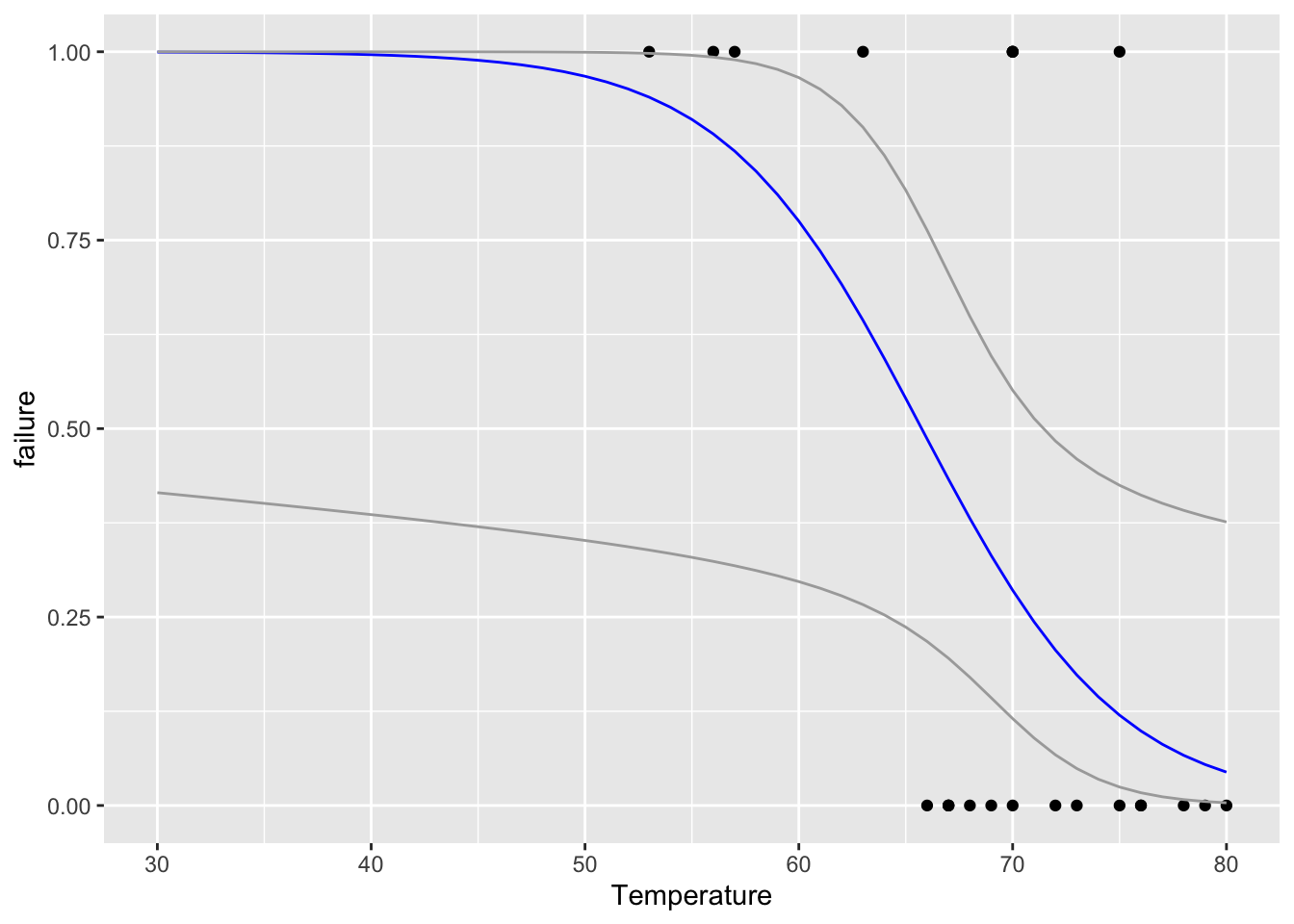

The prediction even at this lowest level of confidence is an unacceptably high probability of failure

Check assumptions:

x <- predict(m1)
y <- resid(m1) 
fig19_4 <- binnedplot(x,y)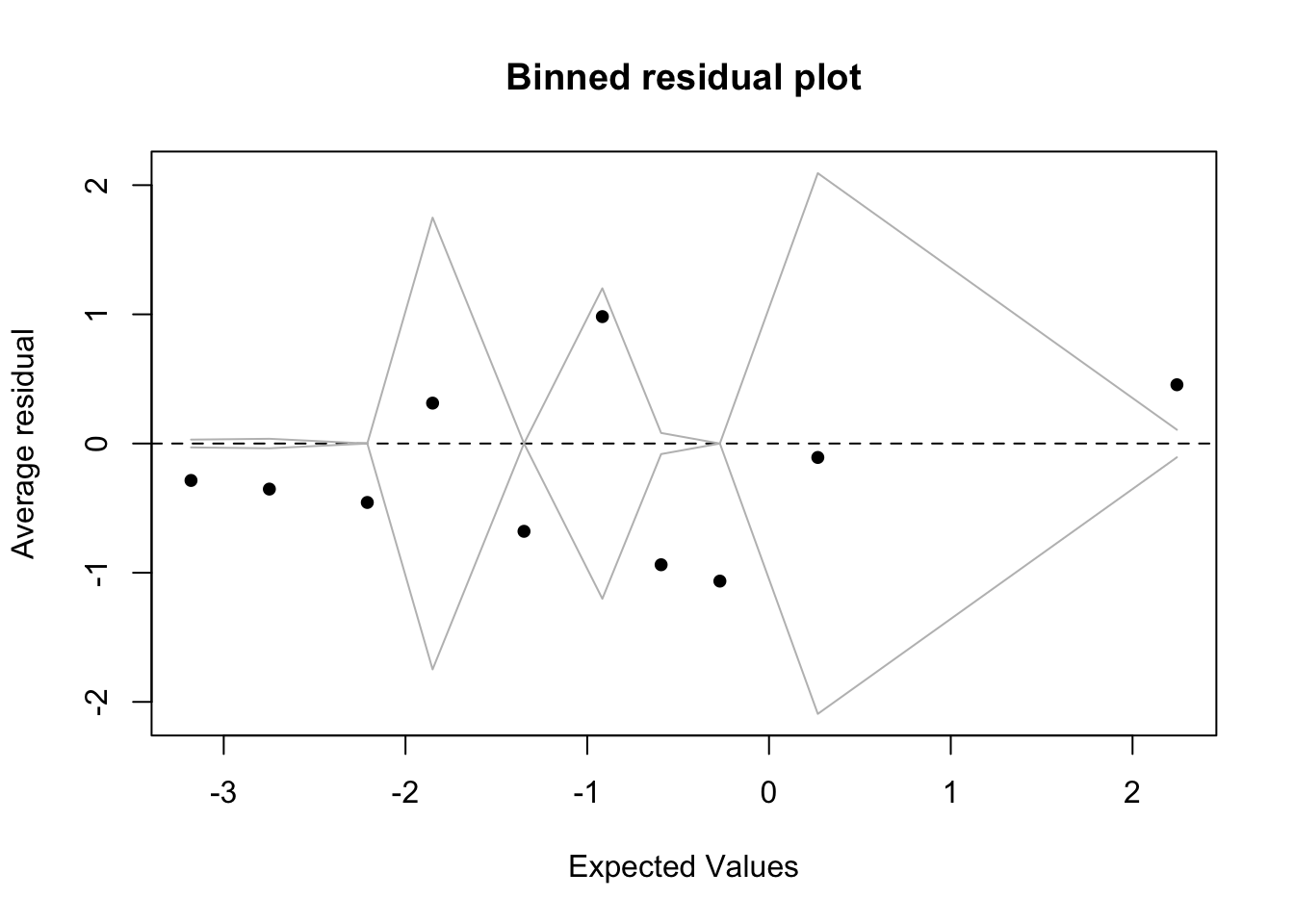

Because most of the values lie outside of the binned zones, the binomial GLM is not a good model for this data (even though they are binary)
Other attempts have been made to model the data (Dalal et al. 1989), but there isn’t yet an ideal solution for this data
Still, even with residuals not supporting a model, it was a poor decision to not even look at any of the data and recommend a launch at on day with much lower launch temperature than ever tested before
The author goes on to talk about how statistics is just one tool that must be combined with others
- For example, these o-rings placed in ice water become brittle too
- Other disciplines could have been consulted too
An imperfect statistical analysis could have saved the lives of seven astronauts

19.3 Recommendations

Make your research reproducible

This can be accomplished through the use of Rmarkdown/quarto to make research reports

A picture is worth a thousands words

Graphs are the best way to present data
Graph data before analyzing it to understand it
Use graphs to assess assumptions/test diagnostics

Keep it simple

Take the time to explore the data and look at estimates/intervals
Get a sense of effect sizes and uncertainties

Consider more than one model

Present 2-3 of the best models to help showcase the uncertain path towards model selection

Attempt the P-free challenger

Focus more on effect sizes and estimates

Report estimates, intervals, and sample sizes

The reproducibility crisis could be combatted by the reporting of these elements in the results section
- This would facilitate meta-analysis

Go back to basics

Understand the basics of error bars and intervals plus how to interpret them

Make a focused plan of analysis

Plan how data will be analyzed in advance
Meet all assumptions

Give P-values the respect they deserve (and no more)

If assumptions are not met, you end up with mushy p-values
The use of p-values should be implemented when all assumptions are met and the satisfaction of all conditions that they depend on so that the values are as meaningful as possible

Focus on repeatability, not small p-values

No matter how small a p-value (or how high the level of confidence), the result can still be a false positive
Scientific results are truly established when it is shown that they are repeatable
Author says that science values novelty too much at the expense of establishing a solid foundation

18 GLMs for binary data